Homomorphic Encryption on Mesh smoothing- NSF&IEEE
IEEE preprinted version. Funded by NSF
Abstract
The development of Fully Homomorphic Encryption (FHE) schemes has generated considerable interest in cryptography. In this paper, we examine the problem of performing a polygonal mesh smoothing on encrypted data. Specifically, we focus on two tasks: developing a polygonal mesh smoothing algorithm under FHE, as well as computing the difference of efficiency of two homomorphic schemes using the identical mesh smoothing algorithm. Due to the high overhead of homomorphic computation, the implementation of the mesh smoothing algorithm was restricted to a naïve Laplacian smoothing approach. We first test low polygons triangular mesh structures on the order of a few thousand vertex points. We construct a working custom implementation of the Laplacian smoothing algorithm that works in both the homomorphic schemes of Cheon-Kim-Kim-Song (CKKS) and Paillier. By taking advantage of CKSS batched computation, we show that it was more efficient than the older Paillier cryptosystem. Lastly, we perform smoothing on encrypted datasets with multiple iterations across the surface of the mesh. By using these methods, we demonstrate the viability of using high-level FHE, not just CKKS, for large scale cloud based mesh smoothing computation and other statistical analysis.
Objective
- Examine different schemes and libraries of Fully Homomorphic Encryption.
- Evaluate methods of surface smoothing that can be utilize with FHE.
- Determine a naïve approach of Laplacian smoothing in CKKS and Paillier.
Background
- Only some arithmetic computations can be done with FHE (multiplication and addition).
- FHE comes with a high overhead, thus having costly computations.
- Homomorphic encryption schemes like Paillier has been researched in the use of electronic voting.
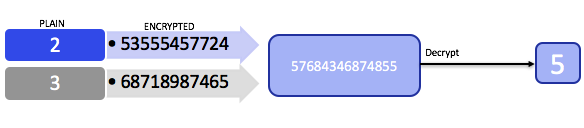
Significance
- Computations on encrypted data does not forsake privacy that may be identifiable to a user or a client.
- Cloud services offer more computation resources that may not be available to a user with a normal and convention PC or network.
- Cloud-based data analytics can be achieved using FHE. Information can be sent through a cloud using FHE from various departments and localizations without identifiable records from the clients.
General Theory
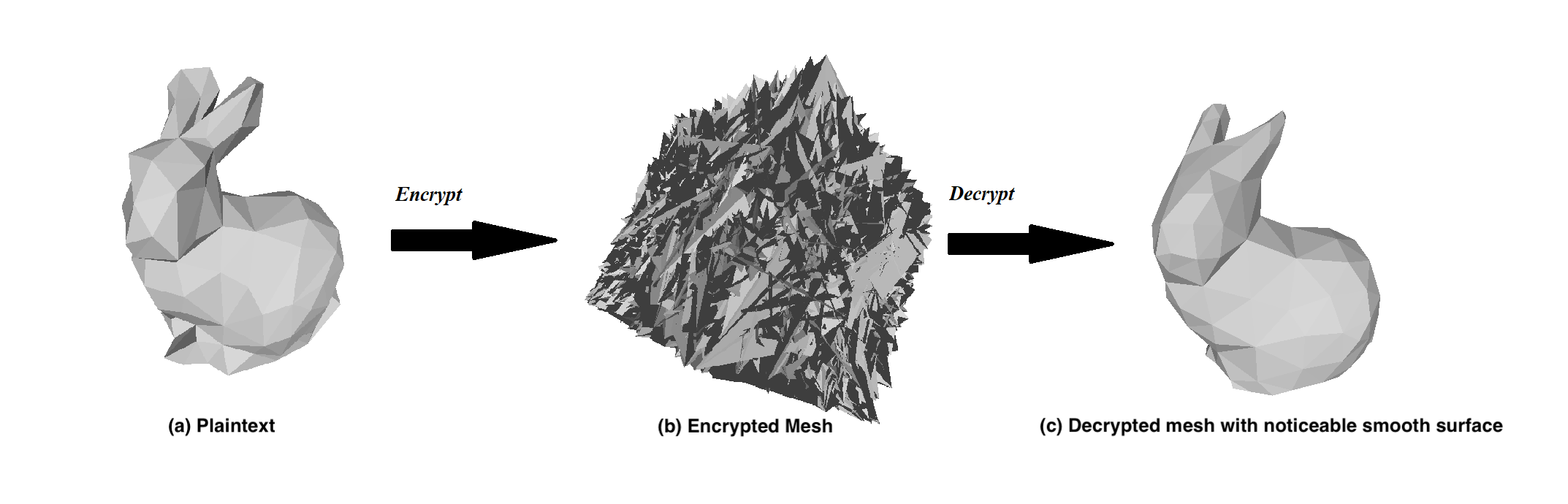
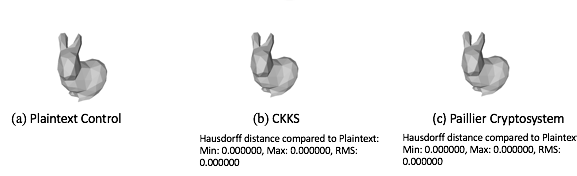
A mesh object is encrypted using a homomorphic encryption scheme. A naïve Laplacian smoothing is implemented at (b) when the data is encrypted using homomorphic encryption. The decrypted mesh (c) should have noticeable smoothen difference than the original.
Softwares and Tools
CKKS
Cheon-Kim-Kim-Song or CKKS is type of scheme introduced in Microsoft SEAL. Unlike BFV, CKKS can handle real numbers with deep approximate computations (floating-point values). CKKS also offers to batch of vectors using SIMD. In this project, we focused on the usage of CKKS due to the real number application. Vertex points are represented in floating-point numbers and not integers, which would use the BFV schema instead. It is possible to use the BFV schema instead, but it would require multiplying the floating-point values by a fixed degree to create an integer value (i.e .001 x 1000 = 1). However, this would result in more computations to be done within thousands and thousands of vertex points.
PAILLIER CRYPTOSYSTEM
Paillier cryptosystem is another schema developed for homomorphic encryption. Compared to the CKKS scheme, the Paillier cryptosystem does not have SIMD for efficient computation. Several research studies have employed Paillier cryptosystem into various applications. For instance, a research study examined the use of Paillier with electronic voting . Paillier is homomorphic only in addition (two ciphertext can be added unbounded) and multiplication (plaintext constant with a ciphertext). For this research, we encrypted the values sequentially and followed an identical smoothing algorithm used in the plaintext control. The Laplacian algorithm functions as intended for the Paillier cryptosystem due to the use of only ciphertext addition and constant multiplication.
OPENMESH
In conjunction with using Paillier and SEAL, this paper used the OpenMesh software library to read in mesh file formats that are either in PLY, OFF, OBJ, STL, and other extensions. This advantage allows us to be able to be universal in applying our smoothing algorithm. However, we controlled the experiment under STL objects.
Algorithm
Many algorithms and methodologies have been researched to create a more robust smoothing algorithm. For instance, the HC algorithm is a robust smoothing algorithm developed for optimized computations. The complexity of arithmetic operations on homomorphic encrypted values limits our demands of a smoothing algorithm. We used a method called Laplacian smoothing, an algorithm to smooth polygonal mesh by allowing a center vertex to move towards the average of its adjacent vertices, as shown in figure below. An undesirable effect of iterative Laplacian smoothing is the shrinkage of the mesh. For this research, we did not primarily focus on the correctness of smoothing in the mesh, but on computation efficiency between two FHE schemes compared to a plaintext control.
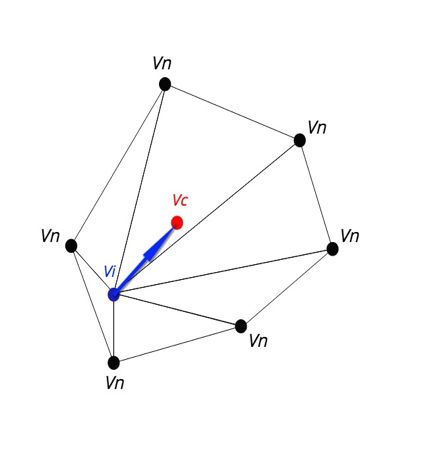
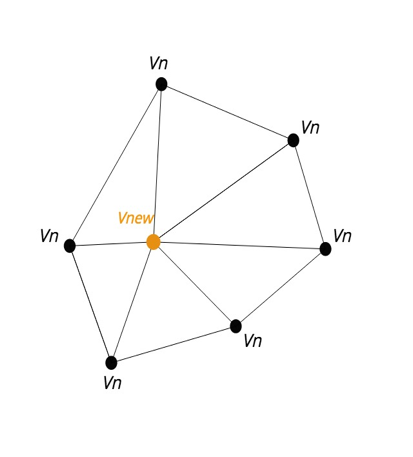
The formula for the Laplacian smoothing follows: $ V_{new} = V_i + k(\Delta V_i) $ where $ 0 < k < 1 $ and $ \Delta V_i$ is defined as:
\[\Delta V_i = V_c - V_i\] \[V_c = (1/N_{V_{N}})\sum V_{N}\]Laplacian smoothing can be performed simultaneously or sequentially. Simultaneous change modifies all vertex \(V_i \rightarrow V_{new}\) in one step (batching). The second variant, sequential smoothing, modifies each \(V_i \rightarrow V_{new}\) immediately after the visit (single). In this case, the computation of \(V_i\) is dependent on the previous calculations of its adjacent points. The simultaneous calculation of all vertex points requires more storage space for holding all old positions \(V_i\) and its neighboring vertices. However, the results are better for simultaneous calculations under homomorphic encryption.
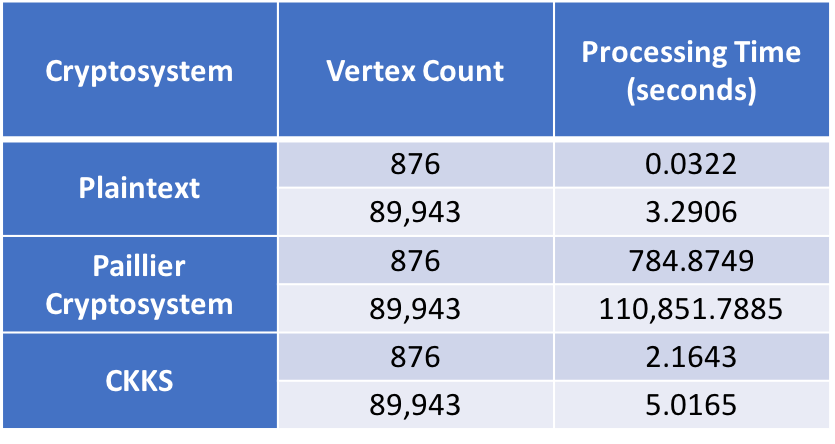
Results
As seen from Fig.(a) to (c), we show that the Paillier, CKKS, and a plaintext algorithm resulted in the same output with 100% accuracy. The difference between the models to the plaintext control was quantified using the Hausdorff distance tool from Meshlab. Hausdorff values of the minimum, maximum, and Root-Mean-Square (RMS) values were 0.000000, showing that the CKKS and Paillier models were identical 100% to the plaintext control.
Plaintext, CKKS, Paillier Crypto
Table
Further results are discussed in the paper.
Discussion
The use of CKKS and Paillier achieves 100% accuracy equal to the plaintext control algorithm. However, the Paillier cryptosystem did not perform adequately during the implementation of the Laplacian smoothing. Large data sets took considerable time to process, indicating that Paillier is not an appropriate scheme for large data sets. We approached the Laplacian smoothing in an individual computer as a proof of concept in its future use in the cloud. Hence, a problem arising from this experiment was the lack of experimentation in large data sets consisting of millions of vertex points. With each adjacent neighbor divided into separate vector arrays, a significant amount of memory was utilized. To address this problem for a future study, more powerful hardware is required to replicate the resources of a cloud server. Likewise, the future direction of the research is to develop a hole-filling algorithm that can be implemented in batch homomorphic encryption.
Link
The code:https://github.com/JustinGausin/homomorphic-encryption-mesh
